Home / Matematika

Bangun Ruang Sisi Datar Materi Matematika Kelas 8 Semester Genap

Bangun Ruang Sisi Datar



Assalamu'alaikum wr. wb.

Selamat pagi anak - anakku sekalian, hari ini kita akan membahas tentang bengun ruang sisi datar.
Ruang lingkup pembahasan kita kali ini yaitu terkait bentuk rangkaian dan rumus bangun ruang tersebut.
Untuk lebih lengkap pelajari juga materi yang sudah ada ada buku paket kalian masing - masing.

1. Kubus


AF = diagonal bidang
AG = diagonal ruang
Beberapa contoh jaring-jaring kubus



Sifat-sifat Kubus:
  1. Memiliki 6 buah sisi berbentuk persegi (bujur sangkar) (ABCD, EFGH, ABFE, CDHG, ADHE dan BCGF)
  2. Memiliki 12 rusuk yang sama panjang (AB,BC,CD,DA,EF,FG,GH,HE,EA,FB,HD,GC)
  3. Memiliki 8 titik sudut yang sama besar (siku-siku) (∠A, ∠B, ∠C, ∠D, ∠E, ∠F, ∠G, ∠H)
  4. Mempunyai 12 diagonal bidang yang sama panjang (AC, BD,EG,HF,AF,EB,CH,DG,AH,ED,BG,CF)
  5. Mempunyai 4 diagonal ruang (AG,BH,CE,DF)

2. Balok

AF= BG = diagonal bidang
AG = diagonal ruang
Beberapa contoh jaring-jaring balok:



Sifat-sifat Balok:
1. Memiliki 6 buah sisi yang terdiri dari 3 pasang sisi yang besarnya sama (ABCD dengan EFGH, EFGH dengan ABCD, ADHE dengan BCGF)
2. Memiliki 12 rusuk yang terdiri dari 3 keleompok rusuk-rusuk yang sama dan sejajar
AB = CD = EF = GH = panjang
BC = FG = AD = EH = lebar
AE = BF = CG = DH = tinggi
3. Memiliki 8 titik sudut
(∠A, ∠B, ∠C, ∠D, ∠E, ∠F, ∠G, ∠H)
4. Mempunyai 12 diagonal bidang
(AC, BD,EG,HF,AF,EB,CH,DG,AH,ED,BG,CF)
5. Mempunyai 4 diagonal ruang yang sama panjang
(AG,BH,CE,DF)

3. Prisma

Prisma adalah bangun ruang yang dibatasi oleh 2 buah bidang berbentuk segi banyak yang sejajar dan sisi-sisi tegak yang berpotongan menurut rusuk-rusuk yang sejajar.
Macam-macam prisma:
  1. Prisma segitiga
  2. Prisma segiempat
  3. Prisma segi-n


Unsur-unsur dari prisma segi-n
1. Jumlah titik sudut = 2n
2. Jumlah bidang = n + 2
3. Jumlah rusuk = 3n
4. Jumlah diagonal bidang = n(n+1)
5. Jumlah diagonal ruang = n(n-3)
Volume = Luas alas x tinggi
Luas Permukaan = ( 2 x luas alas) + jumlah luas sisi tegak

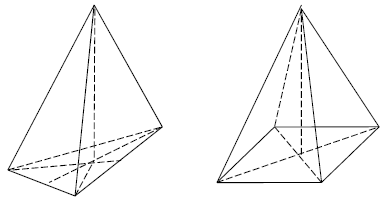
4. Limas

Limas adalah bangun ruang yang dibatasi oleh alas berbentuk segi-n yang kemudian dari sisi alas tersebut dibentuk sisi tegak berbentuk segitiga yang bertemu pada satu titik puncak.



Unsur-unsur limas segi-n
1. Jumlah titik sudut = n + 1
2. Jumlah bidang = n + 1
3. Jumlah rusuk = 2n
4. Jumlah diagonal bidang = n/2(n - 3)
5. Tidak memiliki diagonal ruang
Volume = 1/3 x Luas alas x tinggi
Luas Permukaan = luas alas + jumlah luas sisi tegak