A.
Relasi
1. Pengertian Relasi
Relasi adalah hubungan antara anggota suatu himpunan dengan anggota himpunan
yang lain. Relasi dari himpunan A ke himpunan B adalah menghubungkan
anggota-anggota himpunan A dengan anggota-anggota himpunan B.
Contoh:
Himpunan A ={1,2,3} dan B={A,B,C}. Anggota-anggota himpunan A dan B dapat
dihubungkan dengan relasi yaitu "faktor dari".
2. Cara menyatakan Relasi
Cara menyatakan Relasi dapat dilakukan dengan:
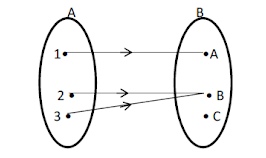
a. Diagram Panah
Contoh di atas dapat dinyatakan dengan diagram panah sbb:
b. Diagram Cartesius
Contoh di atas dapat dinyatakan dengan diagram panah sbb:
c. Himpunan Pasangan Berurutan
Contoh di atas dapat dinyatakan dalam himpunan pasangan berurutan dengan memasangkan
secara berurutan anggota-anggota himpunan A dan anggotaanggota himpunan B
yaitu:
{(1,A), (1,B), (2,B), (3,B), (3,C)}
B.
Fungsi (Pemetaan)
1. Pengertian Fungsi (pemetaan)
Fungsi dari himpunan A ke himpunan B merupakan relasi yang menghubungkan setiap
anggota himpunan A ke tepat satu anggota himpunan B.
Contoh Pemetaan/Fungsi:
Contoh Bukan
Pemetaan/Fungsi:
Tidak semua anggota himpunan A
dihubungkan dengan anggota himpunan B.
2. Domain, Kodomain dan Range
Domain = daerah asal
Kodomain = daerah kawan
Range = daerah hasil
Himpunan A={1,2,3} disebut domain
Himpunan B={A,B,C} disebut kodomain
Hasil pemetaan yaitu {A,B} disebut range
3. Banyaknya Fungsi
Jika banyaknya anggota himpunan A adalah n(A) dan banyaknya anggota himpunan B
adalah n(B) maka:
Banyaknya fungsi yang mungkin dari A ke B = n(B)n(A)
Banyaknya fungsi yang mungkin dari B ke A = n(A)n(B)
Contoh:
Himpunan A ={1,2,3,4} dan B={A,B,C}, carilah:
a. Banyaknya fungsi yang mungkin dari A ke B
b. Banyaknya fungsi yang mungkin dari B ke A
Jawab:
Diketahui:
n(A) = 4 dan n(B) = 3
a. Banyaknya fungsi yang mungkin dari A ke B = n(B)n(A) = 34 = 81
b. Banyaknya fungsi yang mungkin dari B ke A = n(A)n(B) = 43 = 64
4. Notasi dan Rumus Fungsi Linear
a. Notasi fungsi linear
Fungsi linear dinotasikan dengan f : x → ax + b
dimana:
f = nama fungsi
x = anggota daerah asal
ax+ b = bayangan dari x
b. Rumus fungsi linear
f(x) = ax + b
x variabel dan f(x) nilai fungsi
contoh:
f(x) = 2x + 2
Nilai fungsi untuk x = 2 adalah f(2) = 2 x 2 + 2 = 6
c. Grafik fungsi linear
Contoh:
gambarlah grafik fungsi f(x) = 2x + 2
jawab:
tentukan titik potong dengan sumbu x dan y terlebih dahulu:
titik potong dengan sumbu x jika f(x) = 0
0 = 2x + 2 → 2x = -2, maka x = -1
diperoleh titik (-1,0)
titik potong dengan sumbu y jika x = 0
f(x) = 2x + 2 à
f(x) = 2. 0 + 2 = 2
diperoleh titik (0,2)
Buat sumbu koordinat dengan titik-titik (-1,0) dan (0,2) tersebut, kemudian
tarik garis lurus yang melewati titik-titik koordinat tersebut.
5. Korespondensi Satu-satu
Suatu fungsi disebut korespondensi satu-satu jika setiap anggota A tepat
berpasangan dengan setiap anggota B.
Banyaknya korespondensi satu-satu
yang mungkin antara himpunan A dan B adalah:
1 x 2 x 3 x .......x(n-1) x n
Contoh:
Himpunan A={1,2,3} dan himpunan B={A,B,C}. Banyaknya korespondensi satu-satu
yang mungkin untuk himpunan A dan B adalah 1 x 2 x 3 = 6