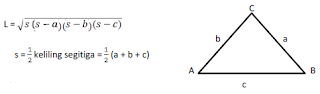A. Segitiga
Segitiga adalah bangun datar yang dibatasi oleh tiga ruas garis dan mempunyai tiga titik sudut.
Jenis-jenis segitiga dapat dibedakan berdasarkan panjang sisi-sisinya atau berdasarkan besar sudut-sudutnya.
1. Jenis-jenis segitiga berdasarkan panjang sisi-sisinya
a. Segitiga sama kaki ⇨ Segitiga yang dua sisinya sama panjang
c. Segitiga sembarang ⇨ Segitiga yang panjang
ketiga sisinya berbeda
-
Ketiga sisinya tidak sama panjang ( AB ≠ BC ≠ CA )
- Ketiga sudutnya tidak sama besar ( ∠A ≠ ∠B ≠ ∠C )
∠A + ∠B + ∠C = 180o
2. Jenis-jenis segitiga berdasarkan besar sudutnya
a. Segitiga siku-siku ⇨ Segitiga yang salah satu
sudutnya 90o
b. Segitiga lancip ⇨ Segitiga yang besar tiap-tiap sudutnya kurang dari 90o
c. Segitiga tumpul ⇨ Segitiga yang salah satu sudutnya lebih besar dari 90o
3. Keliling dan Luas Segitiga
Keliling segitiga ABC (K) = AB + BC + CA
Luas segitiga ABC (L) = 1/2 x alas x tinggi = 1/2 x a x t
Dengan tidak menghitung tingginya tetapi dengan ketiga sisinya, luas segitiga
dapat dicari dengan rumus:
4. Segitiga-segitiga
Sebangun
a. Syarat dua segitiga sebangun
Dua segitiga sebangun jika:
- Panjang sisi-sisi yang besesuaian sebanding
- Susut-sudut yang bersesuaian sama besar
b. Sifat Dua Segitiga
Sebangun
B. TEOREMA PHYTAGORAS
Teorema atau Dalil Phytagoras hanya berlaku pada segitiga siku-siku,
dimana kuadrat sisi miring sama dengan jumlah kuadrat sisi yang lainnya.
Tripel Phytagoras ⇨ Merupakan rangkaian tiga bilangan positif yang merupakan
sisi-sisi dari segitiga sikusiku yang memenuhi dalil Phytagoras. Bilangan yang terbesar merupakan
sisi miringnya.
Untuk segitiga siku-siku di atas tripel Phytagorasnya adalah:
Pasangan
tripel ini berlaku untuk kelipatannya:
misal 6, 8 , 10 merupakan kelipatan dari 3, 4, 5 yang berarti juga merupakan
tripel
Phytagoras.